Homework 3 Math 241/242 Fall 2008

You will probably find it useful to begin with your spreadsheet from Homework 2. Save a copy with a different filename before starting your work.

A: Numerical integration.

Background: Numerical integration is perforce approximate. While there are more accurate methods (take math 541) we cover Riemann sums and the trapezoidal rule.

Using Riemann sums, we approximate the area under a curve by a sum of areas of rectangles. If the x values used are regularly spaced

,

as they are on your spreadsheet, the area is just height*base = f(x_i)*h

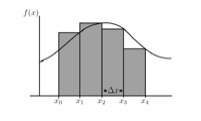
You can find this on your spreadsheet by adding a column as shown below

Since you can factor out the h from the sum, this case did not actually need the other column; you could have summed the second column and multiplied the sum by h to get the approximate integral. For the more complicated cases below, however, the additional column will be useful.

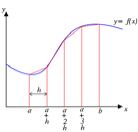
For the trapezoidal rule, you will need to replace the top cell in the new column by ‘=(y(x1)+y(x2))*h/2’ and fill down.

Evaluate approximate values for the following integrals using a partition with 50 x values (a) using left Riemann sums and (b) using the trapezoidal rule.

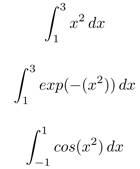
B. Numerical Solution of Differential Equations

Background:

A differential equation is a condition on an unknown function much as an algebraic equation is a condition on an unknown number. Solving the differential equation means finding the unknown function. Consider the following examples of differential equations

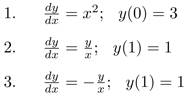
The key observation is that working from a known point, such as the given initial condition, you can approximate the next point using

To solve a differential equation dy/dx = f(x,y) on a spreadsheet, you need the following as the top lines and fill down.

Solve the above three differential equations and have your solution checked in class. For homework, solve the following differential equations.

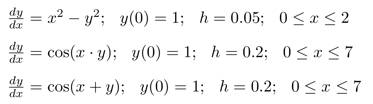
Turn in a workbook with your “code” to solve a differential equation on one sheet. On a separate sheet(s) turn in your answers to the integrals in Part A and screenshots showing the sketches of the solutions to the last three differential equations from Part B. Label what is what in a clear manner.