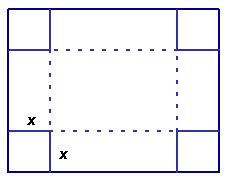
This problem is a classic problem in optimization from Calculus (with a couple new twists). Consider a rectangular piece of cardboard that is 98 cm long and 76 cm wide. You create an open box by cutting square corners (x cm by x cm) from each of the four corners and bending up the sides. This study examines how the volume and surface area of this open box varies as you vary the size of the four corners that you cut out. (Give all answers to 4 significant figures.)

a. Write a function for the volume V(x) of your open box depending on the size x of the square corners that you cut out. What is the domain of this function (from practical physical constraints)? Graph V(x) on its domain, then find the maximum volume and how large a corner you must cut to create this volume.

b. Write a function for the surface area S(x) of your open box depending on the size x of the square corners that you cut out. Give the domain and range of this function. Graph S(x). Is this function only increasing or decreasing (monotonic)?

c. We would like to plot the volume as a function of the surface area without first solving one of these equations for x. If you have placed Parts a. and b. on a single spreadsheet in Excel, then you should be able to plot V (vertical axis) vs S. Find the value of S when V is maximum.